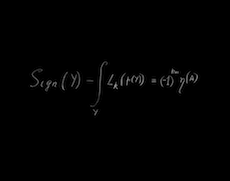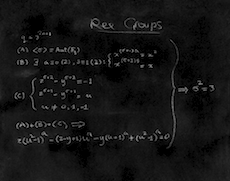writing

As a mathematics student, I spend a lot of time in front of a traditional blackboard watching equation after equation be written and erased, written and erased. While the equations I encounter this way are used to rigorously communicate mathematical concepts to a group of students, they can also be mesmerizing just to look at. In lecture, I often find myself suddenly captivated (distracted?) by the script as it appears in front of me–chalk gliding across the chalkboard as it traces out the curvilinear script of greek letters and other mathematical symbols, sometimes lazily, other times with such fervor it suddenly snaps, waking me from my daze and bringing me back to the classroom.

Over the years, I’ve also noticed that each professor will fill the blackboards in their own unique way. Some choose to place only a single concept at the center of each board before moving on to the next, and others fill each one with scrawling text and diagrams. Much like a writer, each professor curates their exposition according to his or her own taste. What appears on the board are the symbols and surrounding prose that each mathematician has deemed essential to understanding.

When I learned of the exhibit Concinnitas: Prints by Physicists and Mathematicians at Nancy Hoffman Gallery, I was excited to see if this elusive aesthetic could be captured and communicated successfully to an audience of non-mathematicians. Is it possible to really give people who haven’t spent years of study a glimpse of this mathematical aesthetic?

The Project

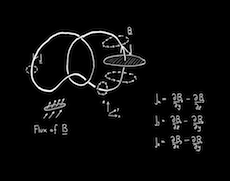
This exhibition is part of the larger Concinnitas Project curated by Daniel Rockmore, a professor of computer science at Dartmouth. The portfolio contains ten prints based on the mathematical drawings of highly-esteemed physicists and mathematicians. Each contributor was asked to produce what they consider to be the “most beautiful mathematical expression.” Their creations were then published as aquatints, white print on black background, reminiscent of the blackboard. The complete collection of works on display can be viewed in the Concinnitas Portfolio.

Selected prints from the Concinnitas Portfolio

The list of contributors is impressive: Michael Atiyah, Enrico Bombieri, Simon Donaldson, Freeman Dyson, Murray Gell-Mann, Richard Karp, Peter Lax, David Mumford, Stephen Smale, and Steven Weinberg (links provided to mathematicians and physicists I recognize). While the list is comprised only of men, this is hardly the fault of the curator as so far there has only been a single female winner of a Fields medal to date, and many of these contributors have either Nobel prizes or Fields medals.

Also included in the project is the Concinnitas Studio, where anyone can submit their own equation representing mathematical beauty. While sparse at the time of this post, I’m looking forward to seeing the list fill out with additional equations and mathematical ideas.

Impression

When I rounded the corner and entered the middle exhibition room of the gallery, I was pleasantly surprised by what I saw. Given that the works were carried out by ten different individuals, I had worried that there might be that usual group show feel: a hodge-podge of works that normally wouldn’t appear all in the same room all cuddled up next to each other, or perhaps fighting each other for space on the walls. Instead, the prints are uniform in size and presentation, though the orientation varied depending on how each ‘artist’ chose to depict his mathemtical concept.

Concinnitas installation view

Concinnitas Installation at Nancy Hoffman Gallery

The space felt uncluttered, allowing me to walk freely from one mathematical concept to the next, unhindered by distractions. Most of the pieces themselves were sparse in presentation, displaying clearly a central concept or idea in mathematics, even if the symbols themselves remained undefined and incomprehensible to all but a few mathematically-inclined individuals who happened to enter the exhibition space. Next to each work was an ‘artist’s statement’ made by the physicist or mathematician who chose the equation. Even with the descriptions, mathematics is such a vast field that a mathematics Ph.D. student such as myself found many of the equations impenetrable even with the accompanying explanation.

But this didn’t bother me. I got to feel that same way I do in the classroom of a prestigious mathematics department, in awe of the great minds that stand at the board in front of me, writing equation after equation. It was exciting to me that this exhibit gave others a glimpse of this same experience.

Further Impressions

Concinnitas gives a sense of a bird’s eye view of mathematics. All of these disparate topics depicted succinctly in the same room give the viewer a chance at gazing upon a vast range of mathematics all at once. Viewing the entire portfolio, we see singular equations, a collection of equations grouped under a heading, graphical structures, and topological drawings. Some equations contain numbers while others only symbols, curvilinear in their elegance or a forest of greek letters.

Even if one does not understand the exact meaning of the symbols, there is something about the tangible nature of the prints that is accessible. Perhaps the number of symbols required to communicate the idea gives some insight into its complexity. That some require a diagram and cannot be summarized by a simple equation betrays the elusivity of the nature of an open problem in mathematics. Some prints contain headings written by the mathematician which I argue detracts from the beauty; others I spoke to seemed to feel that this gave a context and more immediate context for the mathematics.

While it’s impossible for me to step outside of my understanding of mathematics and to see these works as purely aesthetic, what I do know is that I walked away from this exhibit feeling as if I had viewed true works of art. Conceptual art, yes, but the execution of the project was such that it felt like art nonetheless. Not illustration of mathematical ideas, not an artist’s interpretation of a mathematical concept, but unadulterated mathematics as art.

I had the pleasure of seeing Dorothea Rockburne: Drawing Which Makes Itself at MoMA when it was on exhibit. She asked:

“How could drawing be of itself and not about something else?”

What followed was a collection of works made from 1972-1973 that attempt to defy reference to external concepts, meaning, ideas, and objects. The exhibit at MoMA displayed five works from the series: Neighborhood, Nesting, Hartford Installation, Diamond-Parallelogram Overlapping, and Arc. Of these, three (Nesting, Hartford Installation, and Diamond-Parallelogram Overlapping) achieved the goal of remaining entirely self-contained and self-referential, while the other two seemed to leave questions unanswered and miss the mark somewhat.

Rockburne studied mathematics under Max Dehn at Black Mountain College in the 1950s. Beyond obvious geometric shapes and marks, it is not immediately clear from the works to what extent she was exposed to advanced mathematics. A closer investigation suggests that Rockburne was familiar with the concept of constructive proofs in mathematics, and at the very least Dehn’s approach to solving Hilbert’s Third Problem, using notions of scissors-congruence and paper cuts, appears in her work.

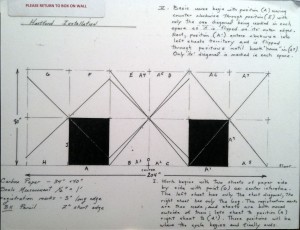
Hartford Installation

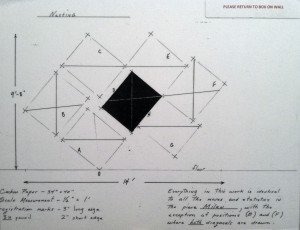
The first work one encounters is Hartford Installation (1972). A sequence of diagonal lines arranged in a symmetric pattern are interrupted by two dark squares, with fingerprints dotting the corners where each of the diagonals intersect. I asked myself how this drawing might accomplish the task of being self-referential. The only clue I had came from watching the accompanying video and reading the adjacent text: the dark squares were carbon sheets that were used to make the marks on the wall, and so the drawing tool is left as part of the drawing itself.

Hartford Installation

Diagram for Hartford Installation

Diagrams are provided for each of the pieces in the series, and these annotations enable the viewer to appreciate and understand the extent to which Rockburne accomplishes her task. In the diagram we are ultimately given the key to deciphering the rest of the drawings in the series (with the exception of Neighborhood): registration marks denoting the position of the corners of the carbon paper at the time of installation are indicated in pencil directly on the wall, with a 3” mark indicating the longer side of the paper and a 2” mark for the shorter side. Along with a description of how the piece is made, these guides orient the viewer and suddenly the element of time enters into the interpretation, one’s eyes tracking the flipping, turning, and marking of the carbon paper on the wall as determined by the registration marks.

Stepping back and reexamining the work, one starts to see what Rockburne means when she looks to make a drawing that refers only to itself. Not only do we see the finished drawing in this installation, but also the tool used to make the drawing (carbon paper) and traces of the algorithm used to compose the work (registration marks). Aside from possibly an instrument used to score the carbon onto the wall (and the chalk used to mark a diagonal line on the carbon in white), everything needed to create the drawing is present: the drawing is itself a proof of its self-referentiality.

Nesting and Diamond-Parallelogram Overlapping

The adjacent work, Nesting, and one of the works installed on the floor, Diamond-Parallelogram Overlapping (not pictured), have similar feels and constructions. Their diagrams indicate how to read the registration marks and the process by which each drawing was made, though once familiar with the language of these drawings (the registration marks, the orientation of the carbon paper and the white lines drawn on diagonals to indicate where the carbon was drawn), the diagrams are not necessary in understanding the construction of the works.

Nesting

Diagram for Nesting

Like Hartford Installation, everything is contained within the drawings themselves. The viewer is not left questioning any aspect of the works: everything is accounted for, and everything seen has a purpose. We are thus left to think about the arrangements, the composition, the freedom that Rockburne has in these constructions. Through working in a rigid framework (flipping carbon paper, marking, following registration marks), we are made aware of the limitation in possibilities and are left to consider the artist’s choices in making these drawings. A certain appreciation for the work is granted that would not befall the typical gallery viewer who walks through an exhibition with hardly a second glance to each of the works presented.

Neighborhood and Arc

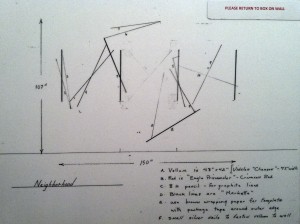
The remaining pieces on display from the Drawings Which Make Themselves series lack this sense of completeness, this notion of proof. In Neighborhood, we see a collection of lines, varying thicknesses and colors, dancing around a piece of vellum tacked on the wall. The diagram indicates the variety of materials used in the drawing, but no mention is given as to how the lines were constructed, according to which rules, or if there was any sort of algorithm at all.

Neighborhood

Diagram for Neighborhood

Even the title, Neighborhood, asks us to try and find reference to some concept outside of the drawing in order to tie together these disparate lines. After studying and coming to understand the previous drawings, I was left wondering how this drawing was still considered self-referential.

In Arc, the final work in the show form this series, Rockburne primarily uses the devices of the first three drawings. The only visible difference is a curved line, perfectly circular and reminiscent of construction by straightedge and compass. Studying the drawing itself gives little clue as to how the new mark was made. The carbon paper is folded under and there do not appear to be any circular marks on the paper itself.

Diagram for Arc

Upon reading the diagram, the viewer learns that a piece of wire, cut to length, has been used to make such a mark, but the wire is nowhere to be seen. While it could be argued that the tools used to construct the drawing do not detract from the feeling of self-reference, especially since the carbon paper is still contained in the drawing, the system does not feel as closed. We sense that some sort of trick was played on us or a rule was broken.

Reaction

Many of the write-ups I read about the show were positive but acknowledged that the exhibition suffered from being cold, austere, and too esoteric, the fate of many mathematically-oriented artworks. But these works are not about mathematics, they are about drawing and art. What struck me about these pieces was not how systematic but in how human they are, how they betray the human struggle against system and material.

Detail of Hartford Installation

Fingerprints dot the registration crosses and we are left to imagine a person, perhaps frustrated, holding a sheet of carbon paper to the wall. Their fingers get messy. They struggle to hold it in place and make the requisite markings. Even after the paper is tacked onto the wall with nails, it is left with ripples and refuses to lay flat. By not dictating that the drawing be left in a pristine condition, we are confronted with the fact that it is a drawing and not a concept after all, the prints on the wall serving as a defiance of association with an idealized geometric form.

The Concinnitas Project and the Art of Mathematics.

Process as Proof: An Interpretation of Dorothea Rockburne's 'Drawing Which Makes Itself' Series