I received my Ph.D. in mathematics from Rutgers University in May 2017 under the direction of Professor Konstantin Mischaikow. My thesis can be found here.
-
Persistence Module Theory
My postgraduate work primarily focued on theoretical aspects of persistent homology and topological data analysis.
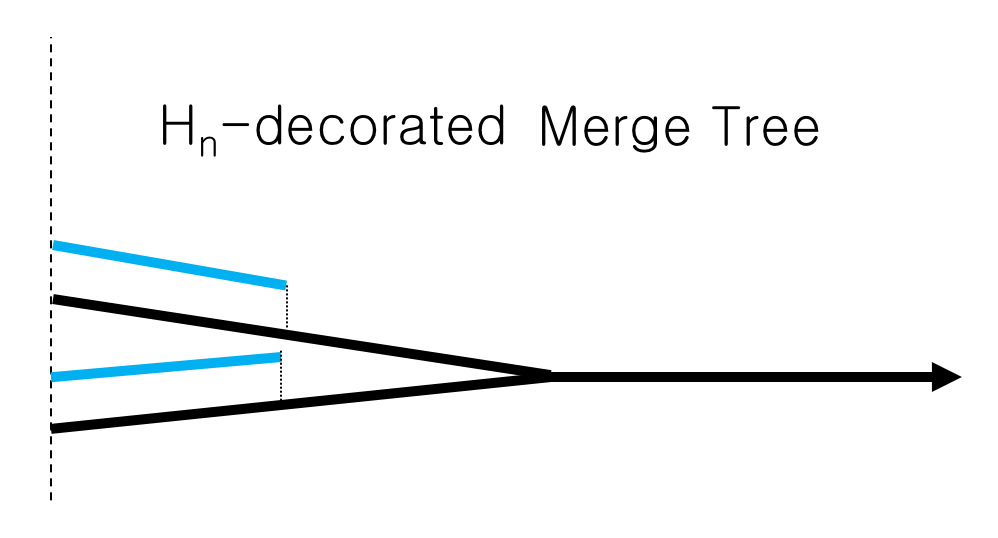On the Stability of Persistence Vineyards
with J. Curry.
In preparation.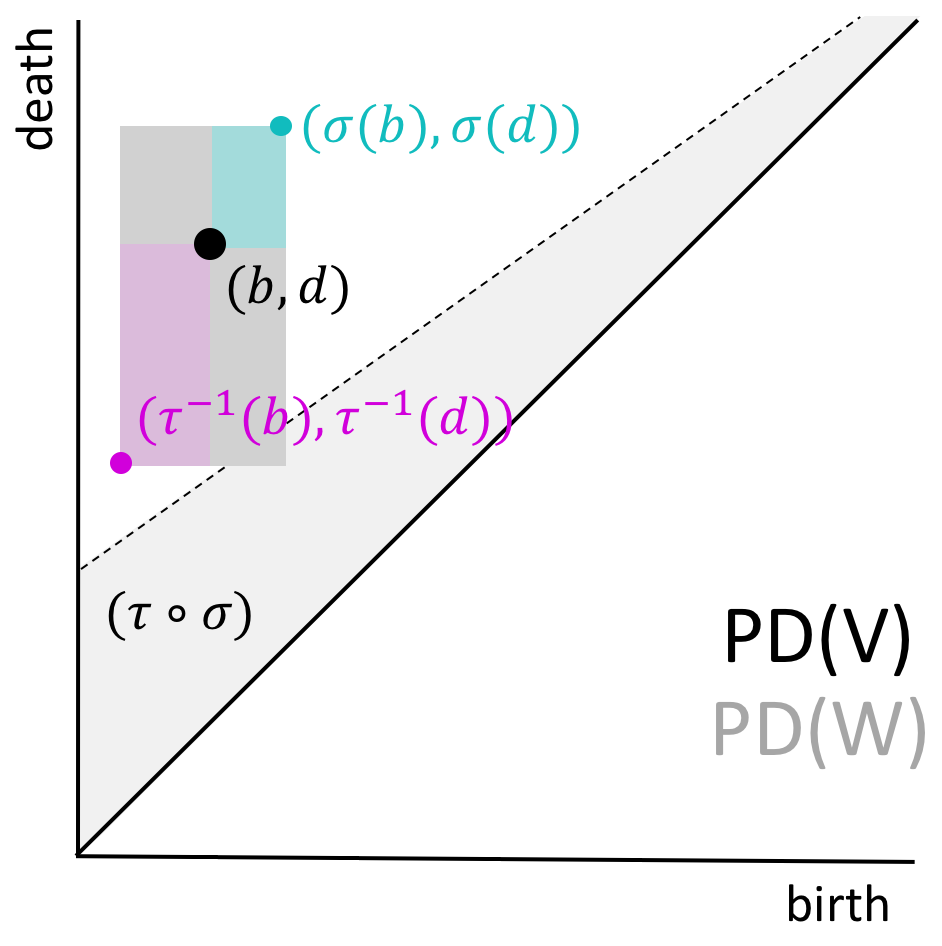
A Comparison Framework for Interleaved Persistence Modules
with S. Harker, M. Kramar, and K. Mischaikow.
JACT | arXiv | AATRN (YouTube) -
Applications of Persistent Homology to Problems in Fluid Dynamics
While a graduate student at Rutgers University, I focused on applications of persistent homology to problems in fluid dynamics, spanning both 2D and 3D fluid flow simulations.
Talk : Studying Fluid Flows with Persistent Homology
Workshop on Topology : Identifying Order in Complex Systems
abstract | video
Studying Homogeneous Charge Compression Ignition with Persistent Homology
with T. Ishihara, P. Dlotko, and K. Mischaikow.
In preparation.
A new relationship between enstrophy and higher order statistics of vorticity in high-resolution DNS of incompressible homogeneous isotropic turbulence
with T. Ishihara, P. Dlotko, M. Kramar, and K. Mischaikow.
In preparation. -
TDA Persistence Explorer
Ever wonder how the points in your persistence diagram correspond to the features in the digital images you’re processing? Download the tda-persistence-explorer app from GitHub and explore your data! Based on the persistence computations from PHAT that utilize discrete Morse theory, this software enables you to encircle persistence points of interest and will then display the corresponding critical cell pairings overlaid on your image, as the screen shot below shows. It also includes a reverse search feature: select a region of interest on the image and the tool will highlight any persistence points with critical cells from their underlying pairings that fall inside.
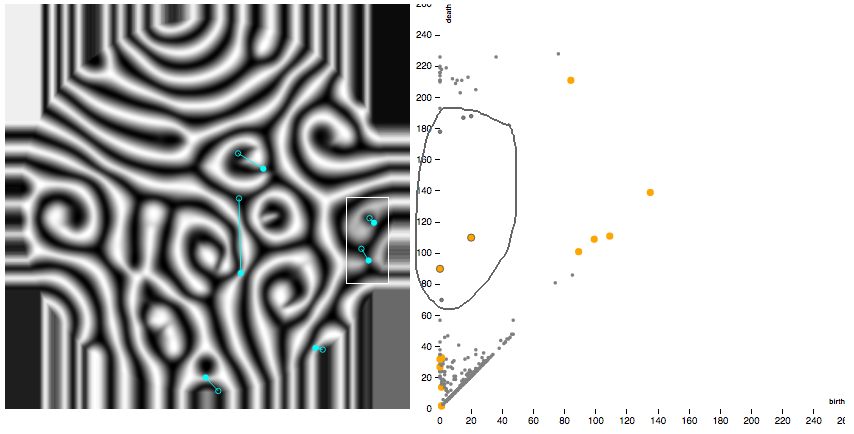
The tool is also great for studying time series of persistence diagrams generated from digital images. The software includes an installation script that will locally install a copy of PHAT and other required dependencies. It also includes a Jupyter notebook that will get you started on some test data. The test images are numerical simulations of Rayleigh-Benard convection flow and were generously provided by the Paul Research Group at Virginia Tech.
-
Undergraduate Work
I was involved in a research project concerning inequalities of singular values of positive semi-definite matrices under the direction of Dr. Raluca Dumitru at the University of North Florida during the Fall 2011 term. We were able to reduce the inequality in question and our results were published in Linear Algebra and its Applications.
PRESENTATION: Imagining the Banach-Tarski Paradox. Presented at the Pi Mu Epsilon National Meeting at MathFest 2011, in Lexington, KY, on August 4, 2011 and received a student speaker award.
ABSTRACT: The Banach-Tarski Paradox states that it is possible to take a solid ball in three-dimensional space, divide it into a finite number of non-overlapping subsets, and then recombine those sets to create two balls with the original size and volume of the first, thus duplicating the sphere. In this presentation, we will examine the precise formulation of duplicative paradoxes, and then follow the development of the Banach-Tarski Paradox from the hollow sphere to the solid ball. With the use of Mathematica pictures and animations throughout the presentation, we will provide a visual interpretation of how such a decomposition is possible, aiding in developing an intuition for the sets involved.
WRITING: Imagining the Banach-Tarski Paradox
An expository writing concerning the development of the Banach-Tarski Paradox, aimed at the advanced undergraduate level. Served as an introduction to LaTeX and Mathematica. Work performed under the direction of Dr. Scott Hochwald at the University of North Florida, Spring 2011.
-
Miscellaneous Mathematical Interests
Mathematics as Metaphor: Mathematics in Contemporary Art. A paper I wrote for a course in Contemporary Art, Fall 2010, under the instruction of Dr. Elizabeth Heuer at the University of North Florida.
ABSTRACT: By examining the relationship between mathematics and art from a historical standpoint, and then looking at the works of Bruce Nauman and specifically his works that use the mathematical subject of topology as motivation, we will see a way in which mathematics may be used to inform contemporary art by way of artistic process and not merely through illustration.
Dueling Scribbles. A small JAVA program that randomly generates two “scribbles” according to a mathematical set of rules (press “d” repeatedly to redraw the scribbles), and the beginnings of an art project on computer generated art and identity. What surprised me in this project was that the nature of the scribbles, though random, seemed to betray the non-randomness of the random number generator used to create them. When drawn, sometimes both will be clumped up in a corner, or both will be splayed out across the page, even though each scribble is instantiated entirely separately from the other.
A Prayer for Math, 2011 (Fib Poem)
Dear
math,
fractals,
spiraling
language of nature,
help me see the world through new eyes.
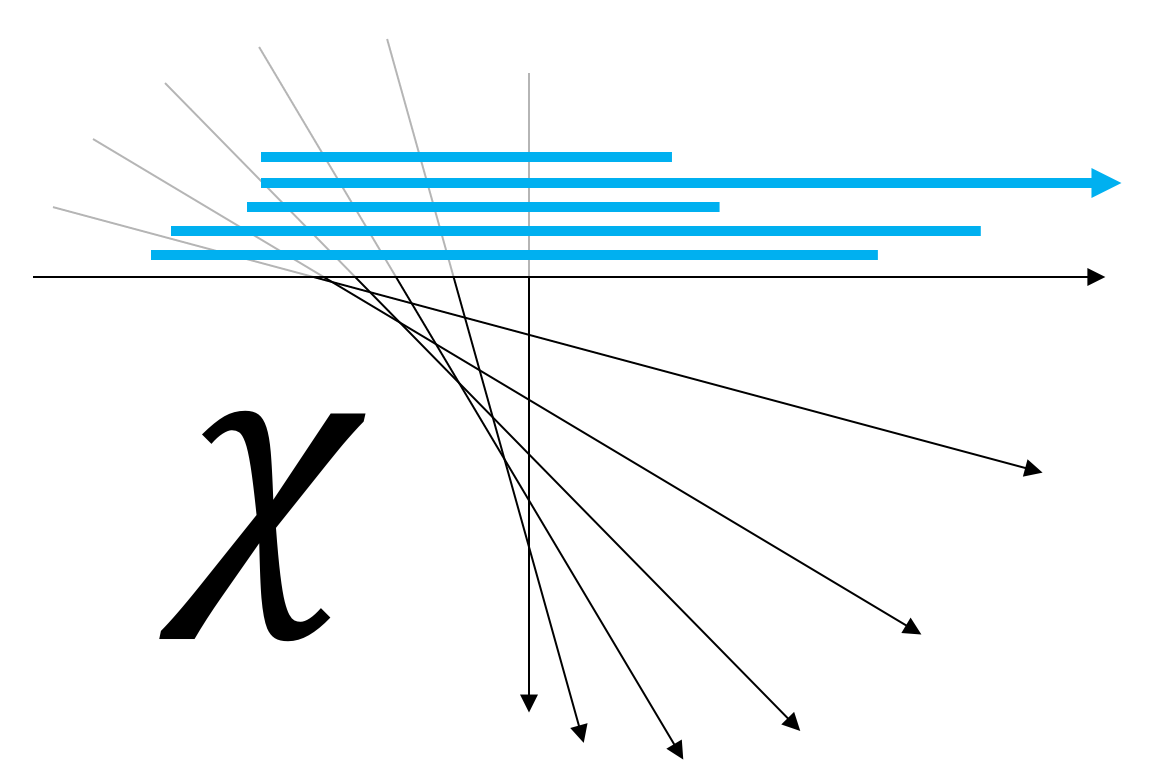Persistent Homology and Euler Integral Transforms
Correlations between the leading Lyapunov vector and pattern defects for chaotic Rayleigh-Bénard convection
Analysis of Kolmogorov Flow and Rayleigh-Bénard Convection using Persistent Homology